数据结构与算法（c 描述）-z6尊龙旗舰厅

19软件工程《数据结构与算法》 第10周安排

讲解第6章的内容 171-187页

重点:

1、图的定义和基本术语

2、图的两种遍历:深度优先和广度优先

后面将要学习的生成树、拓扑排序等都是以遍历为核心的操作

3、图的存储结构:邻接表和邻接矩阵

实验内容于11月10日公布

大家可以根据自己的情况进行相应的预习

师说

哥尼斯堡七桥问题

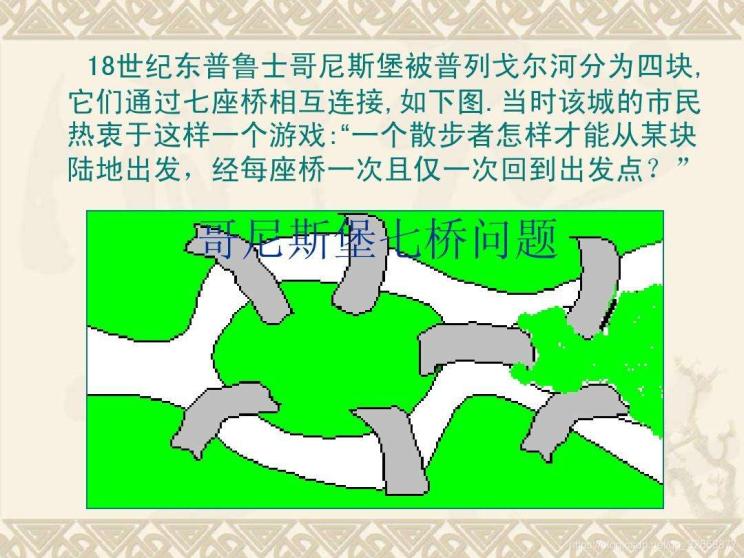
1736年，年仅29岁的数学家欧拉来到普鲁士的古城哥尼斯堡（哲学家康德的故乡，今俄罗斯加里宁格勒）。普瑞格尔河正好从市中心流过，河中心有两座小岛，岛和两岸之间建筑有七座古桥。欧拉发现当地居民有一项消遣活动，就是试图每座桥恰好走过一遍并回到原出发点，但从来没人成功过。欧拉证明了这种走法是不可能的。现在看来，欧拉的证明过程非常简单，但他对七桥问题的抽象和论证思想，开创了一个新的学科:图论(graph)。

欧拉的证明与其说是数学证明，还不如看作是一个逻辑证明。一个曾难住那么多人的问题，竟然是这样一个简单的出人意料的推理，还开创了一个新的学科。欧拉非常巧妙的把一个实际问题抽象成一个合适的数学模型，这种研究方法就是我们应该掌握的数学模型方法。这并不需要运用多么深奥的理论，但能想到这一点，却是解决问题的关键。

现实生活中，与图相关的实际问题非常多:

1、七巧板涂色问题，使用至多 4 种不同颜色对七巧板涂色，要求每个区域涂一种颜色，相邻区域的颜色互不相同。求涂色方案。

2、某公司生产若干种化学制品，其中有些制品如果放在一起可能产生化学反应，因此公司必须将仓库分成相互隔离的若干区，请设计合理的仓库分区。

3、出席某国际会议的六个成员a、b、c、d、e、f，假设a会讲汉语、法语和日语，b会讲德语、日语和俄语，c会讲英语和法语，d会讲汉语和西班牙语，e会讲英语和德语，f会讲俄语和西班牙语，如将此六人分成两组，能否出现同一组内任意两人不能直接交谈的情况?

4、农夫过河问题。一个农夫带着一只狼、一只羊和一筐菜，想从河一边（左岸）乘船到另一边（右岸），由于船太小，农夫每次只能带一样东西过河，但是如果没有农夫看管，则狼会吃羊，羊会吃菜。其给出过河方案。

5、已知软件工程专业专业的核心课程，编制合适的教学计划。

6、旅游出行的路径问题......

思考:下面是一道关于疫情控制的竞赛题，涉及到图和树的数据结构。

题目描述

h 国有 n 个城市，这 n 个城市用 n-1 条双向道路相互连通构成一棵树，1 号城市是首都，也是树中的根节点。

h 国的首都爆发了一种危害性极高的传染病。当局为了控制疫情，不让疫情扩散到边境城市（叶子节点所表示的城市），决定动用军队在一些城市建立检查点，使得从 首都到边境城市的每一条路径上都至少有一个检查点，边境城市也可以建立检查点。但特别要注意的是，首都是不能建立检查点的。

现在，在 h 国的一些城市中已经驻扎有军队，且一个城市可以驻扎多个军队。一支军队可以在有道路连接的城市间移动，并在除首都以外的任意一个城市建立检查点，且只能在 一个城市建立检查点。一支军队经过一条道路从一个城市移动到另一个城市所需要的时间等于道路的长度（单位:小时）。

请问最少需要多少个小时才能控制疫情。注意:不同的军队可以同时移动。

输入输出格式

输入格式:

第一行一个整数 n，表示城市个数。

接下来的 n-1 行，每行 3 个整数，u、v、w，每两个整数之间用一个空格隔开，表示从城市 u 到城市 v 有一条长为 w 的道路。数据保证输入的是一棵树，且根节点编号为 1。

接下来一行一个整数 m，表示军队个数。

接下来一行 m 个整数，每两个整数之间用一个空格隔开，分别表示这 m 个军队所驻扎的城市的编号。

输出格式:

共一行，包含一个整数，表示控制疫情所需要的最少时间。如果无法控制疫情则输出-1。

输入输出样例

输入样例#1:

4

1 2 1

1 3 2

3 4 3

2

2 2

输出样例#1:

3

说明

【输入输出样例说明】

第一支军队在 2 号点设立检查点，第二支军队从 2 号点移动到 3 号点设立检查点，所需时间为 3 个小时。

【数据范围】

保证军队不会驻扎在首都。

对于 20%的数据，2≤ n≤ 10；

对于 40%的数据，2 ≤n≤50，0<_!--10^5；<-->

对于 60%的数据，2 ≤ n≤1000，0<_!--10^6；

对于 80%的数据，2 ≤ n≤10,000；

对于 100%的数据，2≤m≤n≤50,000，0

答案: